Methods/Statistics
Sensitivity analysis to estimate bias-corrected validity measures in outcome validation studies under the “all possible cases” assumption in routinely-collected health databases Norihiro Suzuki* Norihiro Suzuki Masataka Taguri Koichiro Shiba Masao Iwagami Takuhiro Yamaguchi
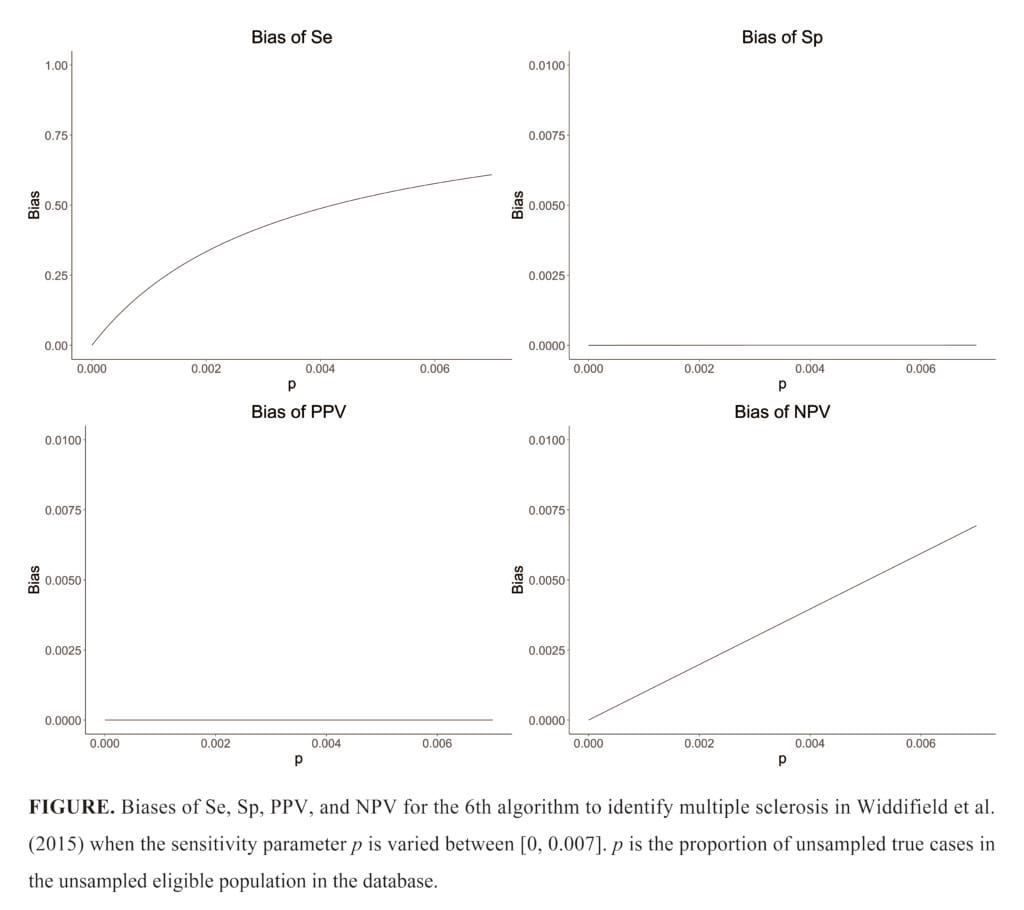
In studies using routinely-collected health databases (e.g., administrative claims databases), it is common to identify the subject’s outcome status by an algorithm (e.g., diagnosis code with a drug prescription). The validity of such an algorithm is assessed with measures such as sensitivity (Se), specificity (Sp), positive predictive value (PPV), and negative predictive value (NPV), based on the result of a validation study comparing the algorithm’s outcome classification with that of a gold standard. Due to time and financial constraints, researchers often use a subset of the study population in the database for validation, particularly for rare outcomes, with a sampling method under the “all possible cases” (APC) assumption—where all true cases (the denominator when calculating sensitivity) in the study population are included in the selected subset. This assumption is violated when unsampled true cases exist, which could lead to overestimated validity measures of the algorithm. However, no study has quantitatively assessed how the extent of unsampled true cases might bias the estimated measures. This study first derives formulas for the bias in each measure when the APC assumption is violated. Using these formulas, we propose a sensitivity analysis method to quantify the bias and compute bias-corrected estimates. We also propose an additional sampling approach in validation studies to obtain point and interval estimates of the bias parameters that can be used in the proposed sensitivity analysis. We illustrate that PPV can always be estimated without bias even when the assumption is violated, while the violation leads to overestimated Se, Sp, and NPV. Our applied examples using real-world data demonstrated that Se would be substantially biased as unsampled true cases increased, while Sp and NPV were relatively robust to the violation (See Figure).