Methods/Statistics
Multiverse sensitivity analysis: Examining robustness of multi-level quantile regression on sparse repeated measures Hayden L. Smith* Hayden Smith
Background: Studies have demonstrated infant positioning can influence physiologic states and neurologic development. Objective: to examine the sensitivity of multi-level quantile regression (MLQR) results versus varied approaches in assessing an intervention to improve infant positioning.
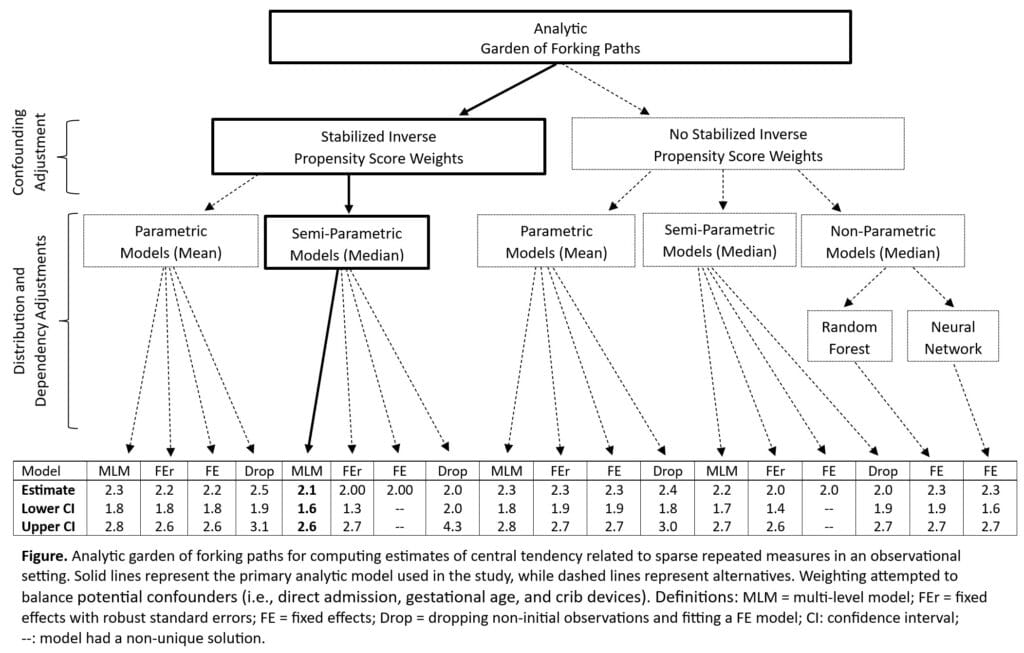
Methods: A pre-post study was conducted at a free-standing children’s hospital in the United States. Study personnel collected patient positioning observations for a period before and after the implementation of the Infant Positioning Assessment Tool (IPAT) into standard practice by NICU nurses. Patients could have had repeated observations collected by study team members during their stay, creating patient level-clusters. The primary statistical model was a MLQR with stabilized inverse propensity score weights to balance covariates. A local analytic garden of forking paths was explored to examine the robustness of the primary results. Garden branches included distributional assumptions, data dependency assumptions, and controlling for possible confounders.
Results: The study included 158 infants with a median of 2 (IQR: 1, 3) repeated observations, represented by a total of 327 observations. One-hundred and sixty-nine observations were in the pre-intervention and 161 in the post-intervention periods. The MLQR model with weights revealed a 2.1 (95% CI: 1.6, 2.8) point median increase in observed positioning scores in the post-period. Figure presents the multiverse sensitivity analysis. Effects and precision estimates appeared robust across statistical methods (estimate range: 2.0-2.5 and confidence interval widths: 0.8-2.2).
Conclusions: Study revealed that within a nominal sized sample with limited repeated observations, results did not vary much by analytic method. Of note, there may have been limited confounding due to study design and a lack of consequential covariance between sparse repeated observations, possibly contributing to the insensitivity of analytic choice.